Cast Nonferrous: Engineering Stress-strain Curve

Abstract: The engineering tension test is widely used to provide basic design information on the strength of materials and as an acceptance test for the specification of materials. In the tension test a specimen is subjected to a continually increasing uniaxial tensile force while simultaneous observations are made of the elongation of the specimen. The parameters, which are used to describe the stress-strain curve of a metal, are the tensile strength, yield strength or yield point, percent elongation, and reduction of area. The first two are strength parameters; the last two indicate ductility.

The engineering tension test is widely used to provide basic design information on images/the strength of materials and as an acceptance test for the specification of materials. In the tension test a specimen is subjected to a continually increasing uniaxial tensile force while simultaneous observations are made of the elongation of the specimen. An engineering stress-strain curve is constructed from the load elongation measurements (Fig. 1).

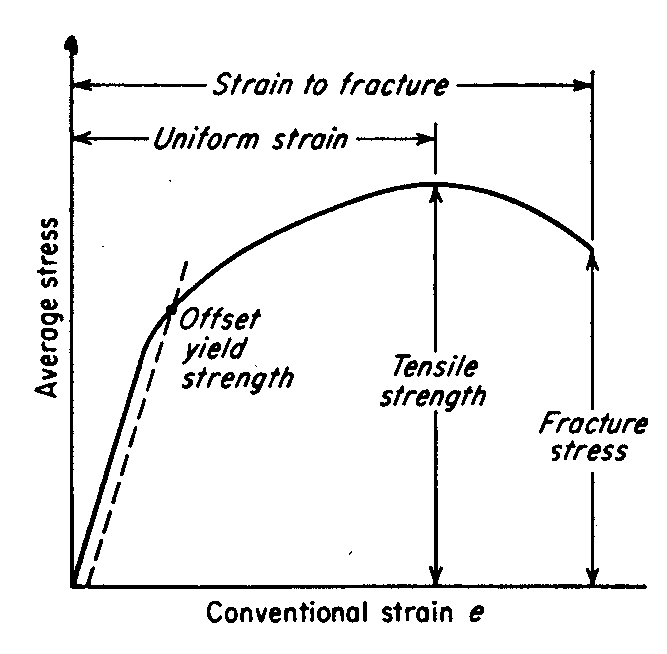
Figure 1. The engineering stress-strain curve

It is obtained by dividing the load by the original area of the cross section of the specimen.

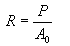(1)

The strain used for the engineering stress-strain curve is the average linear strain, which is obtained by dividing the elongation of the gage length of the specimen, d, by its original length.

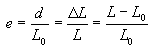(2)

Since both the stress and the strain are obtained by dividing the load and elongation by constant factors, the load-elongation curve will have the same shape as the engineering stress-strain curve. The two curves are frequently used interchangeably.

The shape and magnitude of the stress-strain curve of a metal will depend on its composition, heat treatment, prior history of plastic deformation, and the strain rate, temperature, and state of stress imposed during the testing. The parameters, which are used to describe the stress-strain curve of a metal, are the tensile strength, yield strength or yield point, percent elongation, and reduction of area. The first two are strength parameters; the last two indicate ductility.

The general shape of the engineering stress-strain curve (Fig. 1) requires further explanation. In the elastic region stress is linearly proportional to strain. When the load exceeds a value corresponding to the yield strength, the specimen undergoes gross plastic deformation. It is permanently deformed if the load is released to zero. The stress to produce continued plastic deformation increases with increasing plastic strain, i.e., the metal strain-hardens. The volume of the specimen remains constant during plastic deformation, A·L = A₀·L₀ and as the specimen elongates, it decreases uniformly along the gage length in cross-sectional area.

Initially the strain hardening more than compensates for this decrease in area and the engineering stress (proportional to load P) continues to rise with increasing strain. Eventually a point is reached where the decrease in specimen cross-sectional area is greater than the increase in deformation load arising from strain hardening. This condition will be reached first at some point in the specimen that is slightly weaker than the rest. All further plastic deformation is concentrated in this region, and the specimen begins to neck or thin down locally. Because the cross-sectional area now is decreasing far more rapidly than strain hardening increases the deformation load, the actual load required to deform the specimen falls off and the engineering stress likewise continues to decrease until fracture occurs.

Tensile Strength

The tensile strength, or ultimate tensile strength (UTS), is the maximum load divided by the original cross-sectional area of the specimen.

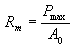(3)

The tensile strength is the value most often quoted from the results of a tension test; yet in reality it is a value of little fundamental significance with regard to the strength of a metal. For ductile metals the tensile strength should be regarded as a measure of the maximum load, which a metal can withstand under the very restrictive conditions of uniaxial loading. It will be shown that this value bears little relation to the useful strength of the metal under the more complex conditions of stress, which are usually encountered.

For many years it was customary to base the strength of members on the tensile strength, suitably reduced by a factor of safety. The current trend is to the more rational approach of basing the static design of ductile metals on the yield strength.

However, because of the long practice of using the tensile strength to determine the strength of materials, it has become a very familiar property, and as such it is a very useful identification of a material in the same sense that the chemical composition serves to identify a metal or alloy.

Further, because the tensile strength is easy to determine and is a quite reproducible property, it is useful for the purposes of specifications and for quality control of a product. Extensive empirical correlations between tensile strength and properties such as hardness and fatigue strength are often quite useful. For brittle materials, the tensile strength is a valid criterion for design.

Measures of Yielding

The stress at which plastic deformation or yielding is observed to begin depends on the sensitivity of the strain measurements. With most materials there is a gradual transition from elastic to plastic behavior, and the point at which plastic deformation begins is hard to define with precision. Various criteria for the initiation of yielding are used depending on the sensitivity of the strain measurements and the intended use of the data.

1. True elastic limit based on micro strain measurements at strains on order of 2 x 10^-6 in | in. This elastic limit is a very low value and is related to the motion of a few hundred dislocations.
2. Proportional limit is the highest stress at which stress is directly proportional to strain. It is obtained by observing the deviation from the straight-line portion of the stress-strain curve.
3. Elastic limit is the greatest stress the material can withstand without any measurable permanent strain remaining on the complete release of load. With increasing sensitivity of strain measurement, the value of the elastic limit is decreased until at the limit it equals the true elastic limit determined from micro strain measurements. With the sensitivity of strain usually employed in engineering studies (10^-4in | in), the elastic limit is greater than the proportional limit. Determination of the elastic limit requires a tedious incremental loading-unloading test procedure.
4. The yield strength is the stress required to produce a small-specified amount of plastic deformation. The usual definition of this property is the offset yield strength determined by the stress corresponding to the intersection of the stress-strain curve and a line parallel to the elastic part of the curve offset by a specified strain (Fig. 1). In the United States the offset is usually specified as a strain of 0.2 or 0.1 percent (e = 0.002 or 0.001).

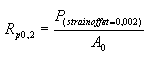   (4)

A good way of looking at offset yield strength is that after a specimen has been loaded to its 0.2 percent offset yield strength and then unloaded it will be 0.2 percent longer than before the test. The offset yield strength is often referred to in Great Britain as the proof stress, where offset values are either 0.1 or 0.5 percent. The yield strength obtained by an offset method is commonly used for design and specification purposes because it avoids the practical difficulties of measuring the elastic limit or proportional limit.

Some materials have essentially no linear portion to their stress-strain curve, for example, soft copper or gray cast iron. For these materials the offset method cannot be used and the usual practice is to define the yield strength as the stress to produce some total strain, for example, e = 0.005.

Measures of Ductility

At our present degree of understanding, ductility is a qualitative, subjective property of a material. In general, measurements of ductility are of interest in three ways:

1. To indicate the extent to which a metal can be deformed without fracture in metalworking operations such as rolling and extrusion.
2. To indicate to the designer, in a general way, the ability of the metal to flow plastically before fracture. A high ductility indicates that the material is "forgiving" and likely to deform locally without fracture should the designer err in the stress calculation or the prediction of severe loads.
3. To serve as an indicator of changes in impurity level or processing conditions. Ductility measurements may be specified to assess material quality even though no direct relationship exists between the ductility measurement and performance in service.

The conventional measures of ductility that are obtained from the tension test are the engineering strain at fracture ef (usually called the elongation) and the reduction of area at fracture q. Both of these properties are obtained after fracture by putting the specimen back together and taking measurements of L_f and A_f .

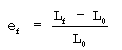	(5)
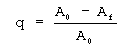	(6)

Because an appreciable fraction of the plastic deformation will be concentrated in the necked region of the tension specimen, the value of e_f will depend on the gage length L₀ over which the measurement was taken. The smaller the gage length the greater will be the contribution to the overall elongation from the necked region and the higher will be the value of e_f. Therefore, when reporting values of percentage elongation, the gage length L₀ always should be given.

The reduction of area does not suffer from this difficulty. Reduction of area values can be converted into an equivalent zero-gage-length elongation e₀. From the constancy of volume relationship for plastic deformation A*L = A₀*L₀, we obtain

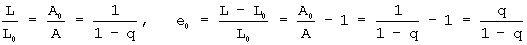(7)

This represents the elongation based on a very short gage length near the fracture.

Another way to avoid the complication from necking is to base the percentage elongation on the uniform strain out to the point at which necking begins. The uniform elongation e_u correlates well with stretch-forming operations. Since the engineering stress-strain curve often is quite flat in the vicinity of necking, it may be difficult to establish the strain at maximum load without ambiguity. In this case the method suggested by Nelson and Winlock is useful.

List of Articles - KTN Knowledge Base